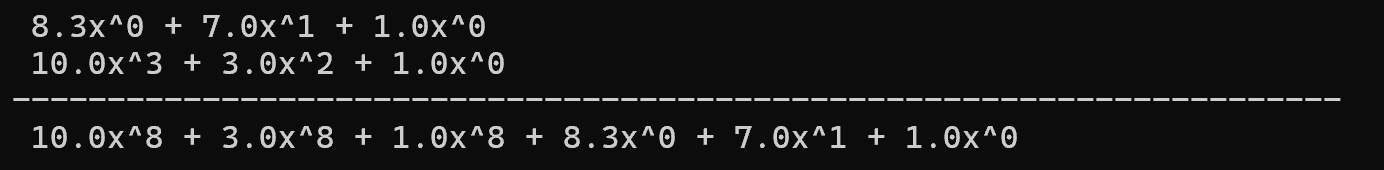배열의 응용: 다항식 표현

unhyepnhj 2024. 7. 5. 19:52

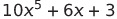
을 예시로 설명

1. 모든 계수를 배열에 저장하는 방법

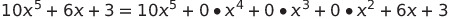
예시 다항식을 위와 같이 다시 쓸 수 있다.

모든 차수에 대한 계수 값들의 리스트인 (10, 0, 0, 0, 6, 3)을 배열 coef에 저장하고 다항식의 차수는 변수 degree에 저장하면, 하나의 다항식이 하나의 degree 변수와 하나의 coef 배열을 필요로 하므로 이들을 묶어 구조체를 만들고 이 구조체를 사용하여 하나의 다항식을 표현할 수 있다.

#define MAX_DEGREE 101	//다항식 최대 차수+1

typedef struct {
	int degree;	//차수
	float coef[MAX_DEGREE];	//계수 배열
} polynomial;

void main() {
	polynomial a = { 5, {10, 0, 0, 0, 6, 3} };
}

이 방법의 장단점은 아래와 같다.

pros	cons
- 직관적으로 이해하기 쉬우며 - 다항식 연산 시 같은 차수의 계수를 찾기에 용이하므로 - 알고리즘이 간단해짐	- 계수가 0인 항이 많은 희소 다항식의 경우 공간 낭비됨

2. 계수가 0이 아닌 항만을 하나의 전역 배열에 저장하는 방법

계수가 0이 아닌 항들을 (계수, 차수)의 형식으로 구조체 배열에 저장하여 표현할 수 있다. 예시 다항식의 경우 ((10, 5), (6, 1), (3, 0))으로 표현되며, 이 방식에서는 하나의 배열에 하나 이상의 다항식을 저장할 수 있다.

#define MAX_TERMS 101

struct{
	float coef;
    	int expon;
} terms[MAX_TERMS];
int avail;

먼저 (계수, 차수) 쌍을 구조체로 선언하고 이 구조체의 배열을 생성한 뒤, 이 배열을 사용하여 다항식을 표현한다.

이 방법의 장단점은 아래와 같다.

pros	cons
- 배열 내 항의 총 개수가 MAX_TERMS를 넘지만 않으면 많은 다항식을 저장 가능	- 하나의 다항식이 시작되고 끝나는 위치를 가리키는 인덱스 변수들을 관리해야 함 - 차수를 저장해야 하므로 - 다항식에 따라서는 계수만 저장하는 첫 번째 방식보다 저장 공간을 더 많이 사용할 수 있음 - 다항식 연산의 구현이 좀 더 어려워짐

프로그램 3.2 다항식 덧셈 프로그램#1

- 첫 번째 방법으로

#include<stdio.h>
#define MAX(a,b) (((a)>(b)?(a):(b)))
#define MAX_DEGREE 101

typedef struct {
	int degree;
	float coef[MAX_DEGREE];
} polynomial;

polynomial poly_add1(polynomial a, polynomial b) {
	polynomial c;
	int Apos = 0, Bpos = 0, Cpos = 0;	//배열 인덱스
	int degreeA = a.degree;
	int degreeB = b.degree;
	c.degree = MAX(degreeA, degreeB);

	while (Apos <= a.degree && Bpos <= b.degree) {
		if (degreeA > degreeB) {	//a항이 고차
			c.coef[Cpos++] = a.coef[Apos++];
			degreeA--;
		}
		else if (degreeA == degreeB) {	//차수 동일
			c.coef[Cpos++] = a.coef[Apos++] = b.coef[Bpos++];
			degreeA--;
			degreeB--;
		}
		else{	//b항이 고차
			c.coef[Cpos++] = b.coef[Bpos++];
			degreeB--;
		}
	}
	return c;
}

void print_poly(polynomial p) {
	for (int i = p.degree; i > 0; i--)
		printf("%3.1fx^%d + ", p.coef[p.degree - i], i);
	printf("%3.1f\n", p.coef[p.degree]);
}

int main(void) {
	polynomial a = { 5, {3,6, 0, 0, 0, 10} };
	polynomial b = { 4, {7, 0, 5, 0, 1} };
	polynomial c;

	print_poly(a);
	print_poly(b);
	c = poly_add1(a, b);

	printf("--------------------------------------------------\n");
	print_poly(c);
	return 0;
}

프로그램 3.3 다항식 덧셈 프로그램#2

- 두 번째 방법으로

#include<stdio.h>
#include<stdlib.h>
#define MAX_TERMS 101

typedef struct {
	float coef;
	int expon;
} polynomial;
polynomial terms[MAX_TERMS] = { {8.3},{7, 1}, {1,0}, {10,3}, {3,2}, {1,0} };
int avail = 6;

//정수 두 개 비교
char compare(int a, int b) {
	if (a > b) return '=';
	else return '<';
}

//다항식에 새로운 항 추가
void attatch(float coef, int expon) {
	if (avail > MAX_TERMS) {
		fprintf(stderr, "항의 개수가 너무 많음");
		exit(1);
	}
	terms[avail].coef = coef;
	terms[avail].expon = expon;
	avail++;
}

//C=A+B
void poly_add(int As, int Ae, int Bs, int Be, int* Cs, int* Ce) {
	float tempcoef;
	*Cs = avail;
	while (As <= Ae && Bs <= Be)
		switch (compare(terms[As].expon, terms[Bs].expon)) {
		case '>':	//A차수>B차수
			attatch(terms[As].coef, terms[Bs].coef);
			As++;
			break;
		case '=':	//A차수=B차수
			tempcoef = terms[As].coef + terms[Bs].coef;
			if (tempcoef)
				attatch(tempcoef, terms[As].expon);
			As++;
			Bs++;
			break;
		case '<':	//B차수>A차수
			attatch(terms[Bs].coef, terms[As].coef);
			Bs++;
			break;
		default:
			break;
		}
	for (; As <= Ae; As++) //A의 나머지 항들 이동
		attatch(terms[As].coef, terms[As].expon);
	for (; Bs <= Be; Bs++) //B의 나머지 항들 이동
		attatch(terms[Bs].coef, terms[Bs].expon);
	*Ce = avail - 1;
}

void print_poly(int s, int e) {
	for (int i = s; i < e; i++) 
		printf("% 3.1fx^%d +", terms[i].coef, terms[i].expon);
	printf("% 3.1fx^%d\n", terms[e].coef, terms[e].expon);
}

int main(void) {
	int As = 0, Ae = 2, Bs = 3, Be = 5, Cs, Ce;
	poly_add(As, Ae, Bs, Be, &Cs, &Ce);
	print_poly(As, Ae);
	print_poly(Bs, Be);
	printf("----------------------------------------------------------------------\n");
	print_poly(Cs, Ce);

	return 0;
}